A

Your helper

Monday, February 23, 2015

Heat and Internal Energy,Work and Heat in Thermodynamic Processes,The Laws of Thermodynamics,Adiabatic ,Isothermal,Isobaric,Isochoric process and their pressure volume diagram,otto cycle and its power stroke as adiabatic process.

Heat and Internal Energy
Internal energy is all the energy of a system that is associated with its microscopic components—atoms and molecules—when viewed from a reference frame at rest with respect to the center of mass of the system

It is associated to the degree of Freedom of an atom or group of atoms.These degree of freedom can be translational,rotational ,vibrational  which we will deal later in this page.
Thermal energy can be interpreted as that part of the internal energy associated
with random motion of molecules and, therefore, related to temperature. Bond energy is the
intermolecular potential energy. Therefore,{ Internal energy} ={ thermal energy+ bond energy} Although this breakdown is presented here for clarification with regard to other books, we will not use these terms because there is no need for them.


Heat is defined as the transfer of energy across the boundary of a system due to a temperature difference between the system and its surroundings.
When you heat a substance, you are transferring energy into it by placing it in contact with surroundings that have a higher temperature. Such is the case, for example, when you place a pan of cold water on a stove burner. The burner is at a higher temperature than the water, and so the water gains energy. We shall also use the term heat to represent the amount of energy transferred by this method.


Work and Heat in Thermodynamic Processes
In thermodynamics, we describe the state of a system using such variables as pressure, volume, temperature, and internal energy. As a result, these quantities belong to a category called state variables. For any given configuration of the system, we can identify values of the state variables. (For mechanical systems, the state variables include kinetic energy K and potential energy U.) A state of a system can be specified only if the system is in thermal equilibrium internally. In the case of a gas in a container, internal thermal equilibrium requires that every part of the gas be at the same pressure and temperature.
A second category of variables in situations involving energy is transfer variables. These variables are zero unless a process occurs in which energy is transferred across the boundary of the system. Because a transfer of energy across the boundary represents a change in the system, transfer variables are not associated with a given state of the system, but with a change in the state of the system. In the previous sections, we discussed heat as a transfer variable. For a given set of conditions of a system, there is no defined value for the heat. We can only assign a value of the heat if energy crosses the boundary by heat, resulting in a change in the system. State variables are characteristic of a system in thermal equilibrium. Transfer variables are characteristic of a process in which energy is transferred between a system and its environment.
In this section, we study another important transfer variable for thermodynamic systems—work.
Consider a gas contained in a cylinder fitted with a movable piston as shown above.At equilibrium, the gas occupies a volume V and exerts a uniform pressure P on the cylinder’s walls and on the
piston. If the piston has a cross-sectional area A, the force exerted by the gas on the piston
is F = PA.
Now let us assume that we push the piston inward and compress the gas
quasi-statically, that is, slowly enough to allow the system to remain essentially in
thermal equilibrium at all times. As the piston is pushed downward by an external
force F =-F ˆj through a displacement of dr = dyˆj  in vector notation since the displacement is to the positive y axis direction.Look at the above figure b.
The work done on the gas is
where we have set the magnitude F of the external force equal to PA because the piston
is always in equilibrium between the external force and the force from the gas.
For this discussion, we assume the mass of the piston is negligible. Because Ady is the change in volume of the gas dV, we can express the work done on the gas as
If the gas is compressed, dV is negative and the work done on the gas is positive. If the gas expands, dV is positive and the work done on the gas is negative. If the volume remains constant, the work done on the gas is zero. The total work done on the gas as its volume changes from Vi to Vf is given by the integral of Equation
As show below
To evaluate this integral, one must know how the pressure varies with volume duringthe process.
In general, the pressure is not constant during a process followed by a gas, but
depends on the volume and temperature. If the pressure and volume are known at
each step of the process, the state of the gas at each step can be plotted on a graph
called a PV diagram, as in Figure below

 This type of diagram allows us to visualize a process through which a gas is progressing. The curve on a PV diagram is called the path taken between the initial and final states.
Note that the integral in Equation
is equal to the area under a curve on a PV diagram. Thus, we can identify an important use for PV diagrams
As Figure in blue suggests, for our process of compressing a gas in the cylinder, the
work done depends on the particular path taken between the initial and final states:
To illustrate this important point, consider several different paths connecting i and f as shown below
In the process depicted in Figure(a)the volume of the gas is first reduced from Vi to Vf at constant pressure Pi and the pressure of the gas then increases from Pi to Pf by heating at constant volume Vf . The work done on the gas along this path is -Pi(Vf - Vi).In Figure b, the pressure of the gas is increased from Pi to Pf at constant volume Vi and then the volume of the gas is reduced from Vi to Vf at constant pressure Pf . The work done on the gas is -Pf(Vf - Vi), which is greater than that for the process described in Figure a.It is greater because the piston is moved through the same displacement by a larger force than for the situation
in Figure a.
Finally, for the process described in Figure c, where both P and V change continuously, the work done on the gas has some value intermediate between the values obtained in the first two processes. To evaluate the work in this case, the function P(V ) must be known, so that we can evaluate the integral in the equation below:
The energy transfer Q into or out of a system by heat also depends on the process. Consider the situations depicted in Figure below
In each case, the gas has the same initial volume, temperature, and pressure, and is assumed to be ideal. In Figure a, the gas is thermally insulated from its surroundings except at the bottom of the gas-filled region, where it is in thermal contact with an energy reservoir. An energy reservoir is a source of energy that is considered to be so great that a finite transfer of energy to or from the reservoir does not change its temperature. The piston is held at its initial position by an external agent—a hand, for instance. When the force holding the piston is reduced slightly, the piston rises very slowly to its final position. Because the piston is moving upward, the gas is doing work on the piston. During this expansion to the final volume Vf , just enough energy is transferred by heat from the reservoir to the gas to maintain a constant temperature Ti .
Now consider the completely thermally insulated system shown in Figure b above. When the membrane is broken, the gas expands rapidly into the vacuum until it occupies a volume Vf and is at a pressure Pf . In this case, the gas does no work because it does not apply a force—no force is required to expand into a vacuum. Furthermore, no energy is transferred by heat through the insulating wall.The initial and final states of the ideal gas in Figure a above are identical to the initial and final states in Figure b above, but the paths are different. In the first case, the gas does work on the piston, and energy is transferred slowly to the gas by heat. In the second case, no energy is transferred by heat, and the value of the work done is zero. Therefore, we conclude that energy transfer by heat, like work done, depends on the initial, final, and intermediate states of the system. In other words, because heat and work depend on the path, neither quantity is determined solely by the end points of a thermodynamic process.

The First Law of Thermodynamics
The first law of thermodynamics for a closed system was expressed in two ways by Clausius. One way referred to cyclic processes and the inputs and outputs of the system, but did not refer to increments in the internal state of the system. The other way referred to any incremental change in the internal state of the system, and did not expect the process to be cyclic. A cyclic process is one that can be repeated indefinitely often and still eventually leave the system in its original state.
In each repetition of a cyclic process, the work done by the system is proportional to the heat consumed by the system. In a cyclic process in which the system does work on its surroundings, it is necessary that some heat be taken in by the system and some be put out, and the difference is the heat consumed by the system in the process. The constant of proportionality is universal and independent of the system and was measured by James Joule in 1845 and 1847, who described it as the mechanical equivalent of heat.
For a closed system, in any process, the change in the internal energy is considered due to a combination of heat added to the system and work done by the system. Taking \Delta U as a change in internal energy, one writes
\Delta U = Q\, - \, W\,\,\,\,\mathrm{(sign\,convention\,of\,Clausius\,and\,generally\,in\,this\,article)}\, ,
where Q and W are quantities of heat supplied to the system by its surroundings and of work done by the system on its surroundings, respectively. This sign convention is implicit in Clausius' statement of the law given above, and is consistent with the use of thermodynamics to study heat engines, which provide useful work that is regarded as positive.
In modern style of teaching science, however, it is conventional to use the IUPAC convention by which the first law is formulated in terms of the work done on the system. With this alternate sign convention for work, the first law for a closed system may be written:
\Delta U = Q + W\,\,\,\,\mathrm{(sign\,convention\,of\,IUPAC)}\, .
This convention follows physicists such as Max Planck, and considers all net energy transfers to the system as positive and all net energy transfers from the system as negative, irrespective of any use for the system as an engine or other device.
When a system expands in a fictive quasistatic process, the work done by the system on the environment is the product, P dV,  of pressure, P, and volume change, dV, whereas the work done on the system is  -P dV.  Using either sign convention for work, the change in internal energy of the system is:
\mathrm d U = \delta Q - P \, \mathrm d V\,\,\,\,\text{(quasi-static process)},
where δQ denotes the infinitesimal increment of heat supplied to the system from its surroundings.
Work and heat are expressions of actual physical processes of supply or removal of energy, while the internal energy U is a mathematical abstraction that keeps account of the exchanges of energy that befall the system. Thus the term heat for Q means "that amount of energy added or removed by conduction of heat or by thermal radiation", rather than referring to a form of energy within the system. Likewise, the term work energy for W means "that amount of energy gained or lost as the result of work". Internal energy is a property of the system whereas work done and heat supplied are not. A significant result of this distinction is that a given internal energy change ΔU can be achieved by, in principle, many combinations of heat and work.
When we introduced the law of conservation of energy , we stated that the change in the energy of a system is equal to the sum of all transfers of energy across the boundary of the system. The first law of thermodynamics is a special case of the law of conservation of energy that encompasses changes in internal energy and energy transfer by heat and work. It is a law that can be applied to many processes and provides
a connection between the microscopic and macroscopic worlds.
suppose that a system undergoes a change from an initial state to a final state. During this change, energy transfer by heat Q to the system occurs, and work W is done on the system As an example, suppose that the system is a gas in which the pressure and volume change from Pi and Vi to Pf and Vf . If the quantity Q + W is measured for various paths connecting the initial and final equilibrium states, we find that it is the same for all paths connecting the two states. We conclude that the quantity Q + W is determined completely by the initial and final states of the system, and we call this quantity the change in the internal energy of the system. Although Q and W both depend on the path, the quantity Q+ W is independent of the path. If we use the symbol Eint to represent the internal energy, then the change in internal energy delEint can be expressed as
where all quantities must have the same units of measure for energy. Equation above is known as the first law of thermodynamics. One of the important consequences of the first law of thermodynamics is that there exists a quantity known as internal energy whose value is determined by the state of the system. The internal energy is therefore a state variable like pressure, volume, and temperature.
When a system undergoes an infinitesimal change in state in which a small amount
of energy dQ is transferred by heat and a small amount of work dW is done, the internal
energy changes by a small amount dEint. Thus, for infinitesimal processes we can
express the first law as a mathematical differential way
The first law of thermodynamics is an energy conservation equation specifying that the only type of energy that changes in the system is the internal energy E int. Let us investigate some special cases in which this condition exists. First, consider an isolated system—that is, one that does not interact with its surroundings.
In this case, no energy transfer by heat takes place and the work done on the system is zero; hence, the internal energy remains constant. That is, because Q = W = 0,it follows that delE int =0,
and thus Eint, i = Eint, f .We conclude that the internal energy Eint of an isolated system remains constant.
Next, consider the case of a system (one not isolated from its surroundings) that is taken through a cyclic process—that is, a process that starts and ends at the same state. In this case, the change in the internal energy must again be zero, because Eint is a state variable, and therefore the energy Q added to the system must equal the negative of the work W done on the system during the cycle. That is, in a cyclic process,

On a PV diagram, a cyclic process appears as a closed curve. (The processes described in
Figure here
are represented by open curves because the initial and final states differ.) It can be shown that in a cyclic process, the net work done on the system per cycle equals the area enclosed by the path representing the process on a PV diagram.
Some Applications of the First Lawof Thermodynamics:
The first law of thermodynamics that we discussed in the preceding section relates the changes in internal energy of a system to transfers of energy by work or heat. In this section, we consider applications of the first law to processes through which a gas is taken. As a model, we consider the sample of gas contained in the piston–cylinder apparatus in figure shown below

This figure shows work being done on the gas and energy transferring in by heat, so the internal energy of the gas is rising. In the following discussion of various processes, refer back to this figure and mentally alter the directions of the transfer of energy so as to reflect what is happening in the process.
Before we apply the first law of thermodynamics to specific systems, it is useful to
first define some idealized thermodynamic processes. An adiabatic process is one
during which no energy enters or leaves the system by heat—that is, Q = 0. An adiabatic
process can be achieved either by thermally insulating the walls of the system,
such as the cylinder in as shown above or by performing the process rapidly, so that there
is negligible time for energy to transfer by heat. Applying the first law of thermodynamics
to an adiabatic process, we see that
From this result, we see that if a gas is compressed adiabatically such that W is positive,
then  delEint is positive and the temperature of the gas increases. Conversely, the temperature
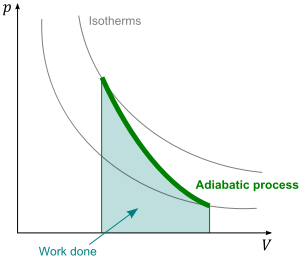
of a gas decreases when the gas expands adiabatically.Adiabatic processes are very important in engineering practice. Some common examples are the expansion of hot gases in an internal combustion engine, the liquefaction of gases in a cooling system, and the compression stroke in a diesel engine as shown at the heading figure.
I will come with the rest of topic in my next page till my subscribe to my page  here.

Advance Mathematical research by Md Tauseef Ibrahim/Abraham Malik

Electronics And Communication by Md Tauseef Ibrahim/Abraham malik
Posted by at No comments:

Saturday, January 10, 2015

Thermodynamics and Different paths in thermodynamics like isothermal,adiabatic,isochoric and isobaric .


Posted by at No comments:
Labels: ,

Types of thermodynamical process like Adiabatic Process, Isochoric Process,Isobaric Process,Isothermal Process,Isothermal expansion of an ideal gas,Adiabatic Expansion of an ideal gas,Adiabatic process,otto cycle ,first law's of thermodynamics ,power stroke of otto cycle is adiabatic Expansion and its relation to mitochondria cell organelle as power house of cell,Petrol and Diesel Engines in Mercedes-Benz,Top 10 petrol cars to buy instead of a diesel



Kinds of Thermodynamic Processes 
In this section we describe four specific kinds of thermodynamic processes that
occur often in practical situations. These can be summarized briefly as “no heat
transfer” or adiabatic, “constant volume” or isochoric, “constant pressure” or
isobaric, and “constant temperature” or isothermal. For some of these processes
we can use a simplified form of the first law of thermodynamics.
Adiabatic Process
An adiabatic process (pronounced “ay-dee-ah-bat-ic”) is defined as one with no
heat transfer into or out of a system;Q = 0.We can prevent heat flow either by
surrounding the system with thermally insulating material or by carrying out the
process so quickly that there is not enough time for appreciable heat flow. From
the first law we find that for every adiabatic process,
U2 - U1 = delU = -W (adiabatic process)

 When a system expands adiabatically, W is positive (the system does work on its
surroundings), so change inU(internal energy)is negative and the internal energy decreases. When a system is compressed adiabatically,W is negative (work is done on the system by its
surroundings) and U increases. In many (but not all) systems an increase of internal
energy is accompanied by a rise in temperature, and a decrease in internal
energy by a drop in temperature as shown in the following figure
The compression stroke in an internal-combustion engine is an approximately
adiabatic process. The temperature rises as the air–fuel mixture in the cylinder is
compressed. The expansion of the burned fuel during the power stroke is also an
approximately adiabatic expansion with a drop in temperature. In Section 19.8
we’ll consider adiabatic processes in an ideal gas.
Isochoric Process
An isochoric process (pronounced “eye-so-kor-ic”) is a constant-volume process.
When the volume of a thermodynamic system is constant, it does no work on its
surroundings. Then W=0 and

In an isochoric process, all the energy added as heat remains in the system as an
increase in internal energy. Heating a gas in a closed constant-volume container is
an example of an isochoric process. The processes ab and cd in Example below are
also examples of isochoric processes. (Note that there are types of work that do not
involve a volume change. For example, we can do work on a fluid by stirring it. In
some literature, “isochoric” is used to mean that no work of any kind is done.)

Example: Comparing thermodynamic processes
The pV-diagram of Fig. below shows a series of thermodynamic processes. In process ab, 150 J of heat is added to the system; in process bd, 600 J of heat is added. Find (a) the internal energy change in process ab; (b) the internal energy change in process abd (shown in light blue); and (c) the total heat added in process acd (shown in dark blue).
 
A pV-diagram showing the various thermodynamic processes.
                                                                SOLUTION

EXECUTE: (a) No volume change occurs during process ab, so the
system does no work:Wab = 0,and so delUab= Qab = 150 J.
(b) Process bd is an expansion at constant pressure, so from Eq.given below

The total work for the two-step process abd is then 
Wabd = Wab + Wbd = 0 + 240 J = 240 J  and the total heat is 
Qabd = Qab + Qbd = 150 J + 600 J = 750 J
Applying Eq.
to abd, we then have
Change(Uabd) = Qabd - Wabd = 750 J - 240 J = 510 J
(c) Because is independent of the path from a to d, the internal energy change is the same for path acd as for path abd:

The Equation 19.5 is the First Law of Thermodynamics as Shown below:
 

                                                Isothermal Process
An isothermal process is a constant-temperature process. For a process to be isothermal, any heat flow into or out of the system must occur slowly enough that thermal equilibrium ismaintained. In general, none of the quantities delU,Q or W is zero in an isothermal process.
In some special cases the internal energy of a system depends only on its temperature,not on its pressure or volume. The most familiar system having this special property is an ideal gas, as we’ll discuss in the next section. For such systems, if the temperature is constant, the internal energy is also constant; delU = 0 and Q=W.That is, any energy entering the system as heat Q must leave it again as work W done by the system Example 19.1, involving an ideal gas, is an example of an isothermal process in which U is also constant. For most systems other than ideal gases, the internal energy depends on pressure as well as temperature, so U may vary even when T is constant.
Example 19.1 An Isothermal expansion of an ideal gas is as following

Figure below shows a pV-diagram for these four processes for a constant amount of an ideal gas. The path followed in an adiabatic process (a to 1) is called an adiabat. A vertical line (constant volume) is an isochor, a horizontal line (constant pressure) is an isobar, and a curve of constant temperature (shown as light blue lines in Fig. below) is an isotherm.
Understanding of These thermodynamical path through a PV Graph is mandatory to solve a lot of Complicated problems in Thermodynamics.
Four different processes for a constant amount of an ideal gas, all starting at state a.For the adiabatic process,Q=0;for the isochoric process,W = 0;and for the isothermal process,Change in U(internal Energy of System) = 0.The temperature increases only
during the isobaric expansion.



 
This adiabatic process is the power stroke in a petrol or diesel engine.It is so special because it is the process that does not involve the transfer of heat into or out of a system Q = 0

So applying  the first law of thermodynamics

\text{(1)} \qquad d U + \delta W = \delta Q = 0,  
For the ideal gas work done is given by
\text{(2)} \qquad \delta W = P \, dV.
\text{(3)} \qquad \Delta U + W = 0

 Hence a positive work done in adiabatic expansion reduces the internal energy of system thus lowering the temperature because internal energy is the function of temperature.Hence when we open a champagne, the pressurized gases inside the bottle expand rapidly and do
work on the outside air W > 0 . There is no time for the gases to exchange heat with their surroundings, so the expansion is adiabatic Q= 0.Hence the internal energy of the expanding gases decreases (ΔU=- W < 0 and their temperature drops. This makes water vapor condense
and form a miniature cloud as shown below.This same phenomenon is also responsible for power providing stroke in petrol engines amazing.The beauty of such adiabatic  process is that is happens very very fast like compression and rarefaction of sound which is also adiabatic.

Adiabatic processes in ideal gases: For an adiabatic process for an ideal gas, the quantities TV^Y-1 and PV^Y are constant. The work done by an ideal gas during an adiabatic expansion can be expressed in terms of the initial and final values of temperature, or in terms of the initial and final values of pressure and volume.

 
 Adiabatic Ideal Gas: Relating V, T, and p

We can derive a relationship between volume and temperature changes for an infinitesimal adiabatic process in an ideal gas:

The above equation Is defined for isochoric process where change in volume is zero,ie where volume is constant throughout the process which can be shown by the following figure:

In Otto cycle (Petrol engine this Adiabatic process is the power stroke) ie this adiabatic process where heat gain or absorbed by the system is zero is the process in the heat engine providing maximum power because it take place very fast such that system is not having enough time to exchange heat with the surrounding.

We describe Otto cycle here.This is the thermodynamical process which undergoes four different processes in a sequential steps hence also called four stroke engine used in lightweight vehicles:

  The Otto Cycle

 

















First of all, what the heck is the Atkinson Cycle and why should we care? Naturally, it's a bit complicated, but basically in a modern Atkinson Cycle engine, the intake valve is held open longer than normal to allow a reverse flow of intake air into the intake manifold and allowing for a smaller compression ratio than the expansion ratio, making the engine more efficient with a slight reduction in overall power. Consult the all-knowing Wiki for more on that.

Most hybrid vehicles' gas-powered engines use an Atkinson Cycle, including the Toyota Prius and GM's 2-Mode Hybrid trucks and SUVs. According to the reliable Lyle Dennis of GM-Volt.com, the Chevy Volt will not use an Atkinson Cycle engine, instead relying on the standard Otto Cycle. For what it's worth, we also know that the Volt's 1.4-liter four cylinder engine will be  controlled and monitored by all manner of electronic gadgetry, and we're sure the automaker has done its homework on making it as efficient as possible.

How Diesel Engine is Different From Petrol Engine And What is the difference between otto Cycle and Steam.?

Today Know About Mercedes Diesel And Petrol Engine:

Powerful, efficient and clean: the latest Mercedes-Benz diesel technology in the CLA. The engine impresses by delivering high pulling power

The 4-cylinder in-line diesel engine with common rail direct injection gives our customers the freedom to explore places around them without worrying about the running costs.
Petrol engine

The highlights of the 4-cylinder diesel engine.

The 4-cylinder diesel engine demonstrate hallmark Mercedes qualities: they are modest when it comes to fuel consumption, are low on emissions and impress with their significantly improved quiet-running characteristics and their reduced vibrations.

In order to keep the engine weight as low as possible, the engine is fitted with a crankshaft with four counterweights and a crankcase bearing with individual bearing caps.

The new CLA 200 CDI has a power output of 100 kW and maximum torque of 300 Nm. As the fourth generation of common-rail diesel technology the engine boast an injection pressure increased to 1800 bar, optimised combustion chambers plus precise solenoid injectors. The high ignition pressure and a turbocharger with a variable nozzle turbine ensure an effortlessly superior torque curve and corresponding pulling power in every engine speed range.
Diesel engine
Further efficiency measures: The diesel drive systems are equipped with the ECO start/stop function which switches off the engine temporarily when the vehicle is stationary. Even greater driving efficiency can be achieved with the help of the standard-fit ECO display which indicates how economically the vehicle is being driven at any given moment. This information can be used to help the driver adopt a driving style which provides for optimum fuel consumption in the current driving situation.

Note : Not conducive for driving in water-logged roads with still water depth more than 25 cm.
The CLA 200 CDI attains its maximum torque of 300 Nm from just 1600 rpm.

Setting the standard: the petrol engine in the CLA combines, dynamic power delivery and effortlessly superior ride comfort with low fuel consumption
and exemplary emission characteristics.
The CLA-Class petrol engine is the best choice for people who want to experience explicit driving performance with phenomenal top speed and acceleration. The 4-cylinder petrol engine in the CLA 200 features homogeneous direct injection, piezo injectors and turbocharging with a displacement of 1991 cc.
Petrol engine
The 4-cylinder petrol engine of CLA 200 comes with 135 kW and a maximum torque of 300 Nm. This engine is extremely low on emissions. The combination of the third-generation Mercedes-Benz high-pressure direct injection system with precise piezo injectors and the enhanced spray-guided combustion process facilitates virtually total combustion and thus allows the fuel to be used particularly efficiently. The variable valve control results in an optimum cylinder charge level which has a beneficial effect on fuel consumption, as do the lower weight, reduced internal friction and ancillaries controlled on an on-demand basis. Turbocharging makes for enhanced responsiveness and higher torque in every engine speed range.

Further efficiency measures. The standard ECO start/stop function also enhances the economic efficiency of the engine. Furthermore, the standard-fit ECO display provides feedback about how efficiently the car is being driven. On the basis of this information, the driver can adjust his or her driving style in order to attain the optimum fuel consumption in the current driving situation.

Effortlessly superior in performance, responsible in consumption

The GL-Class engines offer a potent combination of enhanced performance and reduced consumption. Output has risen by up to 22 percent, for example, while consumption in comparison with comparable-performance vehicles in the previous model series has reduced by up to 20 percent.
The <a class="tooltip" onclick="return false;" href="/content/india/mpc/mpc_india_website/enng/home_mpc/passengercars/tooltips/e/ecostartstop.html" id="/content/india/mpc/mpc_india_website/enng/home_mpc/passengercars/tooltips/e/ecostartstop">ECO start/stop function</a> makes an important contribution to reducing consumption.<br />

6-cylinder diesel engine

An optimised, uprated V6 diesel engine is available for the GL to further reduce fuel consumption and emissions. It is equipped with, amongst other features, third-generation common rail direct injection and also has BlueTEC, an exhaust gas turbocharger and intercooling.

The diesel engine also has a maintenance-free soot particulate filter and meets the requirements of the Euro 6 emissions standard.
  • Huge output: the exhaust gas turbocharger with variable turbine geometry (VTG charger) makes high output as well as high torque possible from a low engine speed. The electrical adjustment feature for the VTG charger gives precise and swift boost pressure control
  • Effective and efficient: the third-generation common rail direct injection with system pressure of up to 1600 bar and piezo injectors as well as dual pilot injection ensure precisely controlled combustion. Up to 5 injections per cycle are possible. This reduces consumption, noise and emissions, while at the same time improving response and handling
  • Clean technology: BlueTEC is a particularly low-emission diesel technology; for this reason the BlueTEC model is one of few vehicles to date to comply with the strict Euro 6 emissions standard
  • Economy as standard: The ECO start/stop function is available as standard The ECO display in the instrument cluster supplies efficiency data on the driver's driving style, offering a motivation to reduce fuel consumption. 

4-cylinder in-line engine

The newly developed 4-cylinder power plant, with a displacement of 1.6 litres, direct petrol injection, variable valve timing and a turbocharger, offers excellent figures
when it comes to both torque and power, plus exemplary quiet-running characteristics, not to mention appropriately low fuel consumption and emissions.

The high-pressure direct injection via precise piezo injectors and an enhanced
combustion process facilitate virtually total combustion and thus higher efficiency, which means that the fuel can be used more efficiently. The variable valve control results in an optimum cylinder charge level and therefore consumption benefits, which also comes courtesy of the lower weight, less internal friction plus ancillaries
controlled as required. And last but not the least, the standard-specification ECO start/stop function raises the efficiency of the engine.

The new petrol engine is developed with the aim of reducing fuel consumption and emissions without compromising on output and ride comfort. The A 180 BlueEFFICIENCY comes with 1595 cc and 90 kW plus a maximum torque of 200 Nm. The petrol engines are low on emission and thus comply with the requirements of emission class Bharat Stage IV.

The 4-cylinder in-line diesel engine with common rail direct injection. This engine is installed transversely and is designed for front-wheel-drive vehicles.

Design

The cylinder head has a special intake port as well as an intake valve lift adapted to the downsized displacement. The engine is installed transversely in the vehicle.

The new engine concept additionally accords due consideration to variants such as right-hand drive models

In order to keep the engine weight as low as possible, the engine is fitted with a crankshaft with four counterweights and a crankcase bearing with individual bearing caps.

In developing the new motor mounts, due consideration was also given to comfortable NVH characteristics for the engine.

Mixture formation:

Common-rail direct injection makes a system pressure of 2000 bar possible. The solenoid valve technology creates the conditions for highly flexible injection timing and smooth engine operation, as well as a high output combined with low fuel consumption and low emissions.

The geometry of the flat combustion chamber design and a low compression ratio minimise untreated emissions, especially of NOx. The maximum ignition pressure of up to 180 bar makes for a high output and low pollutant
emissions.

The single-stage turbocharger ensures a high power output and high torque already at low engine speeds. The VTGturbocharger’s electrical adjustment ensures fast, precise charge-pressure control.

The charge-air ducting has been designed to minimise pressure loss and noise.

Environment:

The exhaust gas recirculation system is modular in design. It is highly efficient on account of low pressure loss, an on-demand cooler bypass and an effective exhaust gas recirculation valve.

The oil and water pumps are activated as required. The belt forces and component weights have been further reduced.

The diesel engine has the ECO start/stop function and ECO display fitted as standard feature. All these characteristics have a positive effect on fuel consumption and emissions.
An Otto cycle is an idealized thermodynamic cycle that describes the functioning of a typical spark ignition piston engine.[It is the thermodynamic cycle most commonly found in automobile engines.

Mercedes-Benz B-Class: petrol engines
The petrol engine was developed with the aim of substantially reducing fuel consumption and emissions without compromising on output and ride comfort. The result: progressive, trendsetting engine technology.
4-cylinder in-line engine. The 4-cylinder powerplant with a displacement of 1.6 litres, direct petrol injection, variable valve timing and a turbocharger offers excellent torque and power and exemplary quiet-running characteristics, not to mention appropriately low fuel consumption and emissions.
The high-pressure direct injection via precise piezo injectors and an enhanced combustion process facilitate virtually total combustion and thus higher efficiency, which means that the fuel can be used more efficiently. Direct injection allows an increase in the compression ratio compared to the previous duct injection, which makes for higher efficiency. The variable valve control results in an optimum cylinder charge level and therefore consumption benefits, which also come courtesy of the lower weight, less internal friction plus ancillaries controlled as required. And last but not least the petrol engine has the ECO start/ stop function and ECO display fitted as standard. Both help the driver to reduce consumption even further. Over and above this the BlueEFFICIENCY measures such as thermal management for an engine warm-up phase that is kept as short as possible, an oil pump controlled as required plus a particularly efficient alternator.

Top 10 petrol cars to buy instead of a diesel

Diesel's reputation has plummeted after new research, revealed in The Sunday Times, found that the fuel is responsible for most of the pollution that causes 29,000 deaths per year in Britain.  

FOR YEARS it's been accepted that the greenest cars are diesel-powered. More fuel efficient and emitting less CO2, they are also fitted with special filters that trap harmful emissions.
But diesel's reputation has plummeted after new research, revealed in The Sunday Times, found that the fuel is responsible for most of the pollution that causes 29,000 deaths per year in Britain. At the same time, technology breakthroughs mean that petrol-powered cars now rival diesels for cost-effectiveness.
The report, commissioned by Defra, the environment ministry, blamed diesel vehicles for a rise in nitrogen dioxide emissions and high levels of tiny toxic particulates that can pass through the lungs to enter every organ in the body. Although much of the pollution is down to buses, lorries and taxis, David Carslaw, of King's College London, a co-author of the report, said that air quality could still be improved if motorists switched from diesel to petrol-powered cars.
“From an air quality point of view it is hard to find a major disadvantage with modern petrol cars, "What most people would say is that petrol is worse than diesel for CO2 emissions. This is still true but even here, a small, modern petrol vehicle can be very low emitting, and will give diesel a run for its money.”The higher purchase cost of some diesel cars threatens to make them redundant against a new generation of small, efficient, turbocharged petrol models. For example, the petrol-powered Ford Fiesta 1.0 Zetec EcoBoost costs £13,895 and returns 65.7mpg. A 1.6 TDCi diesel version of the Fiesta appears much more economical at 85.6mpg but it costs £1,400 more. You would have to travel 81,000 miles to make up the difference in the money you save on fuel.
That's an extreme example but even so, you will generally need to be travelling more than 15,000 miles a year to justify the extra cost of a diesel car. Depreciation is roughly the same, whichever type of engine you choose, according to Cap, a vehicle pricing company.
So if now is the time to switch to petrol cars, here are 10 that will give you just as much for your money as a diesel ‒ and the knowledge that you're doing your bit for air quality, even as the HGVs chug past.

City car Fiat Panda Lounge 0.9 TwinAir 5dr, £11,295 Green credentials: 67.3mpg, 99g/km, tax band A
Of the new generation of small-capacity, turbocharged petrol engines, the Twin Air has received most criticism for failing to get close to its official fuel consumption figure. All the same, it is  economical and brimful of character.

 


 

Posted by at 1 comment:
Labels:
Subscribe to: Posts (Atom)